Sistemas de Ecuaciones

¿Qué es un Sistema de Ecuaciones?

     Para comprender la definición de lo que es un Sistema de Ecuaciones, debemos saber que: 

     Una ecuación lineal o ecuación de primer grado es una ecuación algebraica que involucra una o más variables a la primera potencia y no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia.

     Una ecuación lineal con dos incógnitas "x" e "y" es una expresión de la forma 

a11 x + a12 y =b1

donde a11, a12 y b1 son números reales y las incógnitas x e y tienen por exponente la unidad. Los números a11 y a12 reciben el nombre de “coeficientes” de las incógnitas x e y, respectivamente, mientras b1 se le denomina “termino independiente” de la ecuación.

     Cualquier par ordenado (x,y) que satisfaga la anterior ecuación, se dice que es una solución de ella.

     Toda ecuación lineal con dos incógnitas de la forma (x, y) determina una recta y tienen un número ilimitado de soluciones.

• Vídeo de introducción sobre las ecuaciones 
• Vídeo sobre como solucionar una ecuación de primer grado

     Ya comprendido esto, podemos pasar a definir un sistema de ecuaciones, el cual es un conjunto de dos o más ecuaciones que contiene a dos o más incógnitas, dichas ecuaciones tienen relación entre sí, ya que el valor de las incógnitas satisfacen todas las ecuaciones al mismo tiempo. Este conjunto de ecuaciones se denotan dentro de una llave y resolverlas conlleva hallar el conjunto de valores de cada una de sus ecuaciones.
     Las ecuaciones lineales

     Constituyen un sistema de dos ecuaciones lineales de dos incógnitas x e y, también llamado ecuaciones simultáneas de 2x2
     Cualquier par ordenado (x, y) que satisfaga, simultáneamente, ambas ecuaciones, se dice que es una solución del sistema.
     La representación gráfica de los sistemas de ecuaciones lineales de 2x2 corresponde a dos rectas en el plano cartesiano xy. Estos sistemas tienen solución única si las rectas se intersecan en un punto (x,y), mismo que es la solución del sistema.
     Por ejemplo, en la siguiente figura se muestra la solución gráfica del sistema de ecuaciones

donde cada una corresponde a una recta en el plano cartesiano y la solución al sistema corresponde al punto de intersección (5.4,2.4), lo que significa que el conjunto de valores x=(5,4) e y=(2,4) es la solución del sistema.
   

    Estos sistemas pueden ser resueltos usando tres métodos principales: el método gráfico, el método de sustitución y el método de eliminación o reducción.

•  Método gráfico:

• Método de sustitución:

• Método de eliminación o reducción:

     Gráficamente, una solución del sistema es un punto común a ambas recta P(x,y).

Tipos de sistemas de ecuaciones

     En un sistema de ecuaciones lineales:

• Si las dos rectas se cruzan en un punto, éste representa la solución del sistema. En este caso el sistema de ecuaciones es compatible determinado.
• Si las dos rectas coinciden en todos sus puntos, tiene infinitas soluciones. En este caso el sistema es compatible indeterminado.
• Si las dos rectas son paralelas, no tienen ningún punto común. En este caso el sistema es incompatible y no tiene solución.

    Dicho esto, pasamos a definir con más claridad cada uno de ellos.

1. Sistema compatible determinado: es aquel que tiene una única solución, es decir, las dos rectas se cortan en un sólo punto del plano.
   x = 2, y = 3

     Gráficamente la solución es el punto de corte de las dos rectas.

       2. Sistema compatible indeterminado: es aquel que tiene infinitas soluciones.

     Gráficamente obtenemos dos rectas coincidentes. Cualquier punto de la recta es solución.

      3. Sistema incompatible:  aquí ambas rectas son paralelas, no hay puntos en común, significa que no tiene solución el sistema.

   Gráficamente obtenemos dos rectas paralelas.

Métodos de Resolución de un sistema de ecuaciones

     Se distinguen cinco métodos algebraicos de resolución de sistemas:

• Sustitución

• Igualación

• Reducción

• Gráficos

• Determinantes

    A continuación daremos a conocer en qué consiste cada método de resolución.

     Método de Sustitución

     Este método consiste en aislar una incógnita en una de las ecuaciones para sustituirla en la otra ecuación. De este modo, se obtiene una ecuación con una sola incógnita. Una vez resuelta esta ecuación, se sustituye en alguna de las ecuaciones para hallar la otra incógnita.

Ejemplo:

1. Despejamos x o y en una de las dos ecuaciones. Por ejemplo, y en la primera:

2. Sustituimos este valor en la otra ecuación. En este caso, en la segunda:

Nos queda una ecuación con una sola incógnita, que resolvemos:

3. Calculamos el valor de la otra incógnita:

La solución que se obtiene es:

4. El último paso es comprobar que la solución obtenida está bien:

• Video de ejemplo

     Método de Igualación

     Este método consiste en despejar la misma incógnita en las dos ecuaciones para igualar las expresiones algebraicas obtenidas. Se obtiene, así, una ecuación con una incógnita.

Ejemplo:

1. Despejamos x o y en ambas ecuaciones.

Observa los coeficientes de las incógnitas. Es más cómodo despejar la incógnita que tiene de coeficiente uno, en este caso es la y.

2. Si los primeros miembros son iguales, también lo son los segundos. Por tanto, podemos igualarlos. Obtenemos una ecuación con una sola incógnita, en este caso x.

3. Calcular la otra incógnita. Podemos sustituir en cualquiera de las dos ecuaciones.

La solución del sistema es:

4. Por último, hay que comprobar que la solución cumple las ecuaciones del sistema.

• Video de ejemplo

     Método de Reducción

     Este método consiste en sumar (o restar) las ecuaciones entre sí para eliminar una de las incógnitas. A veces, es necesario multiplicar por algún número las ecuaciones para que, al sumarlas, desaparezca una de las incógnitas.

Ejemplo:

1. Queremos que una de las dos incógnitas tenga en ambas ecuaciones el mismo coeficiente pero con distinto signo. Por ejemplo, la incógnita x en la primera ecuación ha de tener un -2. Para ello transformamos la ecuación en otra equivalente multiplicándola por -2:

2. Por la regla de la suma podemos obtener otra ecuación equivalente, sumando a ambos lados de la ecuación la misma cantidad. Podemos sumar ambas ecuaciones:

3. La otra incógnita se obtiene sustituyendo el valor de y en una de las dos ecuaciones iniciales. Por ejemplo, en la primera:

La solución del sistema es:

4. El último paso es comprobar que la solución está bien.

• Video de ejemplo

     Método Gráfico

     Este método consiste en representar las dos ecuaciones y calcular el punto de corte de las mismas. Este punto es la solución del sistema porque sus coordenadas cumplen ambas ecuaciones.

Ejemplo:

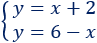
Representación de las gráficas de las dos ecuaciones:

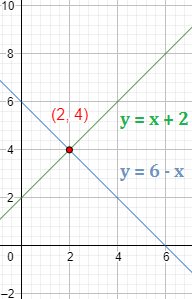
El punto de corte entre las rectas (intersección) es (2,4).

Como la primera coordenada es la $x$ y la segunda es la $y$, la solución del sistema es

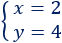
¡Si no hay punto de corte, el sistema no tiene solución!

• Vídeo de ejemplo

     Método de Determinantes

Teorema de Rouchè-Frobenius

    El teorema de Rouché-Frobenius relaciona los rangos de las matrices de coeficientes y ampliada de la representación matricial de un sistema de ecuaciones lineales con el tipo de soluciones de éste.

• El sistema es incompatible si el rango de la matriz de coeficientes \(A\) es distinto del rango de la matriz ampliada \((A|b)\).

• El sistema es compatible si los rangos coinciden. En este caso, si el rango es igual al número de incógnitas (es decir, \(n\)), el sistema es determinado. Si es menor que \(n\), es indeterminado.

Sea \(A·x = b\) la representación matricial de un sistema de \(m\) ecuaciones lineales con \(n\) incógnitas. Entonces,

Cuando es compatible, ejemplo:

     Partiendo de un sistema de ecuaciones aplicaremos el teorema de Rouché- Frobenius

     La matriz ampliada del sistema es

    El rango de esta matriz es 3 porque el determinante de la matriz \(A\) es distinto de \(0\):

Como el rango de \(A\) es máximo, el rango de la matriz ampliada \(A^*\) es también 3.

Por el teorema de Rouché-Frobenius, el sistema es compatible determinado.

 

Cuando es incompatible, ejemplo:

Partiendo de un sistema de ecuaciones

La matriz ampliada del sistema es

El determinante de \(A\) es \(0\), así que su rango es menor que 3. El rango de \(A\) es 2 porque tiene una sub-matriz cuyo determinante es distinto de \(0\):

La matriz ampliada \(A^*\) tiene rango 3 porque tiene una sub-matriz de dimensión 3 con determinante no nulo:

     Como los rangos no coinciden, por el teorema de Rouché-Frobenius, sabemos que el sistema es incompatible. No tiene solución.

Aplicaciones económicas

     Las matemáticas constituyen una herramienta fundamental para entender la dinámica
económica. El uso de la lógica matemática es fundamental y sirve de base a las
interpretaciones del problema económico. 

     Las aplicaciones del álgebra lineal vienen dadas por las ecuaciones que te permiten saber cuándo obtienes ingresos, cuando obtienes pérdidas y cuando haces ventas. Además, permite obtener información acerca de qué tipo de clientes les gustan los productos que ofreces. Incluso, el álgebra lineal puede ayudar a controlar nuestros gastos, estabilizando la economía personal y familiar. En otro aspecto, el álgebra lineal puede emplearse en la macroeconomía, es decir, en la elaboración de presupuestos, gastos e inversiones de un país. Igualmente, pueden establecerse modelos matemáticos específicos para segmentar los sectores económicos y así poder estudiarlos con mayor profundidad.

     Algunos modelos económicos que utilizan sistemas de ecuaciones son:

• Modelo Input-Output de Leontief
• Modelo IS-LM
• Modelo Keynesiano
• Modelo de Oferta y Demanda
• Modelo Markov
• Condición de Hawkins – Simón

• Video de ejercicios económicos con sistema de ecuaciones

Ejercicios para resolver

Ejercicios de sistemas de ecuaciones